MOVIMENTO OSCILATÓRIO
Um movimento oscilatório ocorre quando o sentido do movimento se alterna periodicamente, porém a trajetória é a mesma para ambos os sentidos. Este movimento é o descrito por pêndulos e cordas de guitarras e violões, por exemplo.
A figura abaixo representa uma corda em vibração, observe que mesmo se deslocando para baixo e para cima do ponto de origem ela sempre mantêm distâncias iguais de afastamento deste ponto.
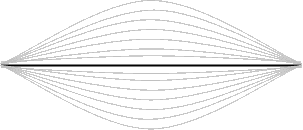
Figura 1: Corda vibrando ( oscilação) Fonte: http://www.sofisica.com.br/conteudos/Ondulatoria/MHS/movpereosc2.php
Considere que o corpo começa a vibrar partindo da linha central mais escura, cada vez que a corda passar por esta linha, após percorrer todas as outras linhas consideradas, dizemos que ela completou um ciclo, uma oscilação ou uma vibração.
Sendo assim, o o movimento periódico, é o intervalo decorrido para que se complete um ciclo é chamado período do movimento (T) e o número de ciclos completos em uma unidade de tempo é a frequência de oscilação (f).
Oscilador Massa-Mola
Figura 2: Modelo de oscilador massa-mola Fonte: http://mundoeducacao.bol.uol.com.br/fisica/oscilador-harmonico.htm
No estudo do movimento harmônico simples, percebe-se que se trata de um movimento periódico e oscilatório. Sendo assim, cabe lembrar que um movimento oscilatório é todo movimento no qual uma mesma evento se repete em intervalos de tempos iguais.
Sendo assim, pode-se caracterizar um oscilador harmônico como sendo o dispositivo da figura acima. Nele tem-se um corpo de massa m sobre sobre uma superfície sem atrito, preso a uma mola helicoidal, ideal, cuja constante elástica vale k. O oscilador encontra-se em equilíbrio na posição O, ou seja, a mola está em seu estado natural.
Caso apliquemos uma força externa sobre o corpo, tentando esticar ou comprimir a mola, e em seguida soltarmos esse corpo, veremos que a massa começa a executar um MHS cujo período vale T. Pense agora que não haja forças dissipativas, o valor x do deslocamento efetuado é chamado de amplitude (A) do MHS. A trajetória retilínea do corpo é orientada; e o ponto O, de equilíbrio, é a sua origem.
Sendo assim, pode-se obter no ponto A com a mola esticada x = +a e com a mola comprimida no ponto B, x = -a. A força .jpg) aplicada é, a cada instante, igual, em valor absoluto, à força elástica , expressa por:
aplicada é, a cada instante, igual, em valor absoluto, à força elástica , expressa por:
.jpg) aplicada é, a cada instante, igual, em valor absoluto, à força elástica , expressa por:
aplicada é, a cada instante, igual, em valor absoluto, à força elástica , expressa por:
Fel = -k.x (lei de Hooke)
O sinal tem significado atrelado ao tipo de força elástica. A força da lei de Hook é do tipo restauradora, ou seja, está sempre orientada para a posição O de equilíbrio.
Figura 3: Descrição do movimento oscilador massa mola. Fonte: http://mundoeducacao.bol.uol.com.br/fisica/oscilador-harmonico.htm
Note que, na posição de equilíbrio, ou seja, quando x = 0, a força elástica é nula; e nos extremos A e B, assume o valor máximo em módulo. Como:
m.γ=-k.x
Sendo T o período do MHS, e começando-se a contar o tempo (t = 0) a partir do ponto extremo B, as figuras seguintes representam as posições da partícula a cada um quarto de período, até completá-lo.
Figura 4: Descrição da velocidade do oscilador massa-mola ponto-a-ponto Fonte: http://mundoeducacao.bol.uol.com.br/fisica/oscilador-harmonico.htm
De acordo com a figura acima, temos:
Nos pontos extremos, a velocidade é nula, pois a partícula está mudando de sentido; e na posição de equilíbrio, a velocidade é máxima.
Mesma descrição é aplicável em outras situações de oscilação. A equação (1) nos mostra que a posição do objeto esta atrelada a uma aceleração que varia com a constante mola e massa da mola. Verifica-se que este movimento oscilatório se repete na horizontal. Usando dos artifícios do cálculo diferencial e transformando a equação (1) em uma equação diferencial sua solução terá uma função de domínio e imagem do tipo cíclica, ou seja, fornecendo valores que se repetem dentro de um intervalo.
A posição do corpo após um impulso em um tempo t é dada por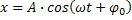
onde: x é a elongação ( variação da posição objeto em função do ponto de retorno ou equilíbrio)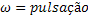 é a frequência de vibração deste movimento oscilatório, A é a amplitude ou elongação máxima do movimento e
é a frequência de vibração deste movimento oscilatório, A é a amplitude ou elongação máxima do movimento e 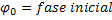 ponto de partida inicial da massa em relação ao ponto de retorno.
ponto de partida inicial da massa em relação ao ponto de retorno.
A velocidade do corpo após após impulso em um tempo t é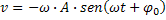
A aceleração do corpo após após impulso em um tempo t é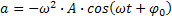
Pendulo Simples
A posição do corpo após um impulso em um tempo t é dada por
onde: x é a elongação ( variação da posição objeto em função do ponto de retorno ou equilíbrio)
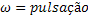 é a frequência de vibração deste movimento oscilatório, A é a amplitude ou elongação máxima do movimento e
é a frequência de vibração deste movimento oscilatório, A é a amplitude ou elongação máxima do movimento e 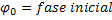 ponto de partida inicial da massa em relação ao ponto de retorno.
ponto de partida inicial da massa em relação ao ponto de retorno. A velocidade do corpo após após impulso em um tempo t é
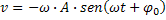
A aceleração do corpo após após impulso em um tempo t é
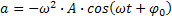
Pendulo Simples
Um pêndulo é um sistema composto por uma massa acoplada a um ponto fixo, que permite sua movimentação livremente. A massa fica sujeita à força restauradora ( semelhante a do sistema massa-mola) causada pela gravidade.
Existem inúmeros pêndulos estudados por físicos, já que estes descrevem-no como um objeto de fácil previsão de movimentos e possibilita inúmeros avanços tecnológicos. Alguns deles são os pêndulos físicos, de torção, cônicos, de Foucalt, duplos, espirais, de Karter e invertidos. Mas o modelo mais simples e que tem maior utilização é o pêndulo simples.
Este pêndulo consiste em uma massa presa a um fio flexível e inextensível por uma de suas extremidades e livre por outra, representado da seguinte forma:
Figura 5: Movimento do pêndulo simples Fonte: http://www.sofisica.com.br/conteudos/Ondulatoria/MHS/pendulo.php
Quando afastamos a massa da posição de repouso e a soltamos, o pêndulo realiza oscilações. Ao desconsiderarmos a resistência do ar, as únicas forças que atuam sobre o pêndulo são a tensão com o fio e o peso da massa m. Desta forma:
Figura 6: Esquema das forças sobre massa no pêndulo Fonte: http://www.sofisica.com.br/conteudos/Ondulatoria/MHS/pendulo.php
A componente da força Peso que é dado por P.cosθ se anulará com a força de Tensão do fio, sendo assim, a única causa do movimento oscilatório é a P.senθ. Então:
No entanto, o ângulo θ, escrito em radianos que por definição é dado pelo quociente do arco descrito pelo ângulo, que no movimento oscilatório de um pêndulo é x e o raio de aplicação do mesmo, no caso, dado por ℓ, assim:
Onde ao trocamos por F:
Assim é pode-se concluir que o movimento de um pêndulo simples não descreve um MHS, já que a força não é proporcional à elongação e sim ao seno dela. No entanto, para ângulos muito pequenos,  , o valor do seno do ângulo é aproximadamente igual a este ângulo.
, o valor do seno do ângulo é aproximadamente igual a este ângulo.
Então, ao considerarmos os caso de pequenos ângulos de oscilação:
Como P=mg, e m, g e ℓ são constantes neste sistema, podemos considerar que:
Então, reescrevemos a força restauradora do sistema como:
Sendo assim, a análise de um pêndulo simples nos mostra que, para pequenas oscilações, um pêndulo simples descreve um MHS.
Como para qualquer MHS, o período é dado por:
e como
O período do pêndulo simples será expresso na formula abaixo:
Assista após leitura da teoria o vídeo abaixo sobre OSCILADOR HARMÔNICO:
PÊNDULO SIMPLES
Após assistir vídeo faça a atividade 6 descrita abaixo:
Atividade 6
Um estudante faz o estudo experimental de um movimento harmônico simples (MHS) com um cronômetro e um pêndulo simples como o da figura, adotando o referencial nela representado. Ele desloca o pêndulo para a posição +A e o abandona quando cronometra o instante t = 0. Na vigésima passagem do pêndulo por essa posição, o cronômetro marca t = 30 s.
a) Determine o período (T) e a frequência (f) do movimento desse pêndulo. b) Esboce o gráfico x (posição) versus t (tempo) desse movimento, dos instantes t = 0 a t = 3,0 s; considere desprezível a influência de forças de atrito. (faça o desenho no papel, tire uma foto e poste sua foto).
OSCILADOR HARMÔNICO: EQUAÇÃO DIFERENCIAL DE SEGUNDA ORDEM
OSCILADOR HARMÔNICO SIMPLES

Anteriormente temos a imagem de uma EDO que modela o movimento do corpo variando sua posição, velocidade e aceleração em torno de ponto de equilíbrio (movimento periódico).
Atividade 7
A partir da equação dada assista os vídeos abaixo e faça o que se pede:
VIDEO 1 RESVOLVENDO EDO SEGUNDA E UM PVI
VIDEO 2 SOLUÇÃO DA EDO DO OSCILADOR HARMÔNICO FORÇADO E AMORTECIDO
Resolva o seguinte exercício:
Uma mola de constante elástica k = 2000 N/m tem sua extremidade fixada na parede, e a outra num carrinho de massa m = 5kg, que pode se movimentar sobre uma superfície plana e sem atrito. A partir da posição de equilíbrio o carrinho é puxado para a direita até que a elongação da mola corresponda ao valor de x = 0,25 metros. Esse valor de elongação dado é valor de elongação máximo, ou seja, A ( amplitude. Depois de solto o carrinho se comporta como um oscilador harmônico simples.
a) Calcule a solução da EDO do oscilador harmônico simples.
b) Determine o período T e a frequência de oscilação desse conjunto.
c) Determine as constantes de fase inicial e frequência de vibração para este caso específico.









Nenhum comentário:
Postar um comentário